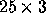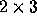, mais l'attribution des données est
différente! Dans la plupart des cas vous allez lire vos matrices ligne
par ligne et vous devez alors préciser l'argument byrow=T,
car byrow=F est la valeur par défaut dans matrix().
La commande dim(Z1) vous donne les dimensions de la matrice.
Essayez aussi Z1+Z2 et t(Z1)%*%Z2 (il s'agit en fait de
la multiplication matricielle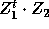 
). Si x et y sont deux vecteurs
de même longueur, as.vector(x%*%y) donne alors le produit scalaire
usuel.
Pour extraire
des éléments d'une matrice: Z1[1,2] donne l'élément (1,2), Z1[,2] la 2ème
colonne, Z1[1,] la 1ère ligne, Z1[,c(1,3)] les colonnes 1 et 3. Les
fonctions rbind() et cbind() sont utiles pour construire des matrices:
écrivez nouveau <- c(4,5) et regardez cbind(Z1,nouveau): cbind()
peut coller des colonnes, rbind() de manière similaire des lignes.
Consultez la documentation de dimnames() pour voir comment on peut donner
des noms aux lignes et colonnes.
Voici quelques autres fonctions concernant les matrices: t() pour la transposée,
eigen() pour calculer des valeurs et vecteurs propres d'une matrice
carrée, chol() pour
la décomposition de Choleski, solve() pour trouver l'inverse et finalement
svd() pour la décomposition en valeurs singulières. Souvent,
vous avez besoin de calculer des statistiques sur des matrices, comme par exemple
trouver la moyenne sur toutes les lignes. Supposez Z de dimension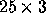 
:
apply(Z,1,mean) vous donne un vecteur contenant les 25 moyennes par ligne.
De la même manière, apply(Z,2,var) donne les variances estimées des
3 colonnes.
Il est possible de créer des matrices de n'importe quelle dimension. Posez z <- 1:30 et Z <- array(z,c(2,3,2)) et regardez comment S-PLUS
présente une matrice de dimension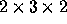 
. Comparez Z[1,,1]
et Z[1,,].